SÉCURITÉ NFC CASHLESS

Introduction

Durant ma troisième année en école d'ingénieurs, j'ai eu la chance de pouvoir travailler avec une entreprise pendant plusieurs mois, dans le but de tester la sécurité de leur solution de paiement. Étant à but éducatif pour moi, cette activité m'a permis de comprendre l'impact que pouvaient avoir les vulnérabilités hardware sur le fonctionnement de notre société. Comme nous allons le voir ici, leur système comportait de nombreuses vulnérabilités. Leur système de paiement a maintenant été mis à jour dans sa totalité (nous ne verrons pas comment dans cet article). L'entreprise a tenu à rester anonyme.

Partie 1 : Présentation du sujet et premières observations

Paypas (nom fictif) propose des services de paiement cashless pour les entreprises souhaitant fidéliser leurs clients. Un peu comme les cartes T-money, elle propose un système de paiement utilisant des cartes NFC rechargeables.

Les cartes cashless ont généralement deux options pour permettre un paiement. La première est d'écrire le montant directement sur la carte, elle est plus vulnérable car elle pourrait permettre la lecture et la modification de ce montant. La seconde option, est d'utiliser un identifiant, mais il faut alors avoir une infrastructure plus complexe qui gère les données de chaque carte.

En rechargeant ma carte, j'ai eu un message m'indiquant d'attendre et de ne pas toucher à la carte, juste après que mon paiement ait été accepté … mais pourquoi ? Était-ce pour récupérer un identifiant ? surement pas, c'était déjà fait depuis longtemps. Pour vérifier le paiement ? Ça n'aurait pas pris autant de temps. Pour écrire le nouveau montant sur la carte, puis le vérifier ? Ça, c'est possible ! De plus, le système de lecture et de recharge ne semblaient pas communiquer ensemble directement.

J'ai alors regardé le montant sur ma carte avant de rentrer chez moi, il y avait 16€. Arrivé chez moi, j'ai utilisé mon ChameleonUltra et ai remarqué qu'il s'agissait d'une carte Mifare Classic 1k. Ce type de carte est surement le plus répandu de nos jours et est victime de nombreuses vulnérabilités vis à vis de la confidentialité, de l'intégrité des données, de la protection contre la duplication, …

Les blocs étant protégés par des clés inconnues, je ne pouvais pas simplement faire une attaque par force brute. J'ai donc utilisé mon Proxmark3 pour aller plus loin.

Partie 2 : Analyse approfondie du support

En premier lieu, j'ai utilisé la commande hf mf info pour en apprendre plus sur cette carte. C'était une carte Mifare classic 1k. Cette carte peut être vulnérable pour de nombreuses raisons (https://www.sidechannel.blog/en/mifare-classic-2/). Les cartes MIFARE Classic utilisent un schéma de chiffrement appelé Crypto1 pour sécuriser les communications et les données stockées sur la carte. Chaque carte est divisée en plusieurs secteurs (16 secteurs pour les cartes 1K, 40 secteurs pour les cartes 4K). Chaque secteur contient 4 blocs (pour les cartes 1K) ou 16 blocs pour certains secteurs des cartes 4K. Chaque bloc a une taille de 16 octets. Exemple de bloc : 5E7A8313640000004006000000000100. Les vulnérabilités sur ces cartes viennent généralement de l'utilisation de clés de chiffrement connues et génériques, et des exploitations sur la génération de valeurs pseudo aléatoire qui comporte souvent des vulnérabilités.

Pour résumer, ces cartes utilisent un chiffrement basé sur Crypto1 et une authentifiaction. Le chiffrement Crypto1 utilisé par les cartes MIFARE Classic vise à sécuriser les échanges de données via une authentification mutuelle et un chiffrement par flux. Cependant, en raison des vulnérabilités de l'algorithme et de la mauvaise gestion des clés par de nombreux systèmes, la sécurité de ces cartes est compromise.

En utilisant une attaque du nom de hardnested, basée sur la faiblesse de génération de nombres aléatoires, et une antenne adaptée à celle de la carte, j'ai pu retrouver toutes les clés en quelques heures.

Dans un autre cas, les clés utilisées n'étaient pas du tout aléatoire, j'ai pu les trouver dans un dictionnaire.

Partie 3 : Lecture de la carte

Premier Dump mémoire

Connaissant les clés, on peut donc lire toute la mémoire.

Dans ce "dump" de mémoire, on lit tout ce qui est écrit sur la carte. Bien sûr, ce n'est pas du texte mais des données écrites en binaire. On les représente en hexadécimal pour plus de lisibilité. Pour quelqu'un qui n'est pas habitué a voir de l'hexadécimal, c'est illisible. Mais pour quelqu'un plus habitué aussi, en fait. Il n'y a ni séquence de début de fichier, ni chaine de caractères, ni rien du tout de lisible. Mais alors ou est écrite la valeur 16? On sait qu'en hexadécimal, 16 est représenté comme 0x10 (0x est le préfixe pour dire que c'est de l'hexadécimal).

En observant bien, on voit qu'il y a plusieurs occurrences de ce fameux 0x10. Mais alors que faire ? Changer la valeur 0x10 par 0x11, puis retourner à la borne pour voir si ça change ? Je n'ai pas choisi de faire ça, je suis retourné à la borne, j'ai utilisé 3€ et j'ai relu la mémoire. Les valeurs 0x10 étaient toujours les mêmes, même avec 13€, c'était donc une fausse piste. En fait, tout était pareil, ou presque … Les blocs 10 et 12, eux avaient changé !

Voici les blocs 10 à 12 pour 16€ :
10 : 5E7A 8313 6400 0000  4006 0000 0000 0100
11 : FA42 5093 C9F2 FF07  8000 FA1F B1EA 0BAE
12 : 4006 0000 BFF9 FFFF  4006 0000 00FF 00FF

La douzième ligne est une succession de "0x4006" et de "0xFFFF-0x4006" Ces données ne sont donc probablement là que pour valider, elles permettent de s'assurer qu'une erreur d'écriture n'altèrent pas les données, il ne faudrait pas qu'un client perde son argent, ou se retrouve avec 500€, tout ça pour une petite erreur d'écriture...

Analyse des données

Voici le bloc 10 pour Les valeurs 16 puis 13 :

13 : 000000a0: 5feb 9513 6400 0000 1405 0000 0000 0100  _...d...........
16 : 000000a0: 5e7a 8313 6400 0000 4006 0000 0000 0100  ^z..d...@.......

Certaines valeurs changent, d'autres non. Avec seulement ces données, il est difficile d'en apprendre plus, je vous invite à essayer de trouver par vous même comment pourraient être stockées ces données, dites vous que c'était une première pour moi aussi !

J'ai alors tenté un autre vecteur d'attaque. Avec une carte NFC chinoise à quelques centimes, on peut modifier les identifiants de la carte, le UID, le ATQA et le SAK. J'ai alors dupliqué à l'identique la carte. Voici un schéma du test alors réalisé :

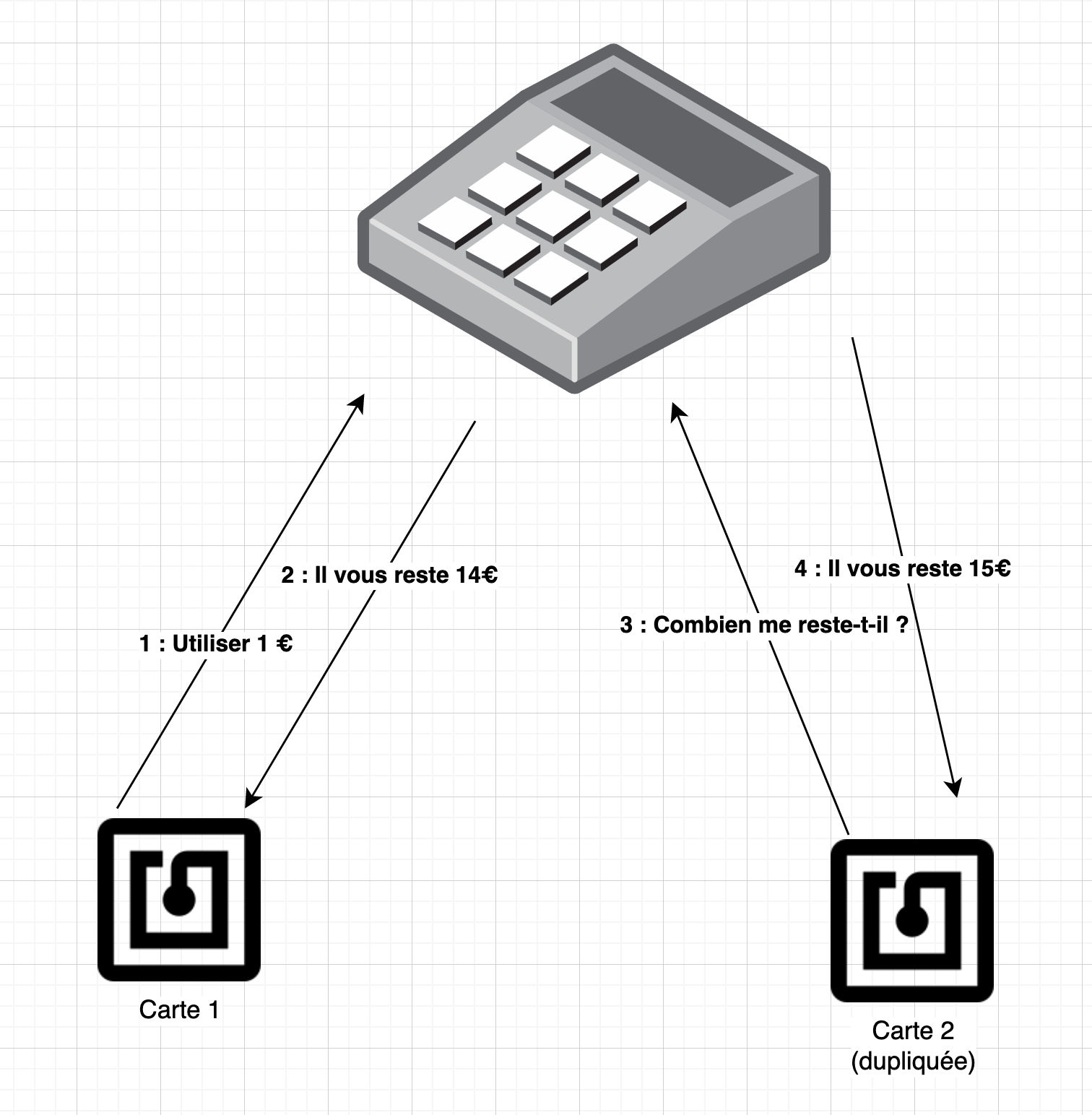
Voici donc une première attaque concrète dont pourrait profiter un attaquant malveillant. Ce qu'il s'est passé, c'est qu'on a deux cartes strictement identiques, et lorsqu'on utilise de l'argent sur une, ça n'affecte pas le montant sur l'autre.

Pour revenir en arrière, j'ai décidé de réaliser une série de mesures pour essayer de trouver comment étaient stockées cette fameuse valeur , dont la valeur 0. Récupérer la valeur associée à 0 permettait de savoir si une opération de multiplication était faite dessus.

0  : 000000a0: 2734 3e26 6400 0000 0000 0000 0100 0100  '4>&d...........
4  : 000000a0: e298 3509 6400 0000 9001 0000 0100 ffff  ..5.d...........
5  : 000000a0: 3e98 3509 6400 0000 f401 0000 0100 ffff  >.5.d...........
6  : 000000a0: bc97 3509 6400 0000 5802 0000 0100 ffff  ..5.d...X.......
7  : 000000a0: fd96 3509 6400 0000 bc02 0000 0100 ffff  ..5.d...........
9  : 000000a0: 4699 3509 6400 0000 8403 0000 0100 ffff  F.5.d...........
10 : 000000a0: 9198 3509 6400 0000 e803 0000 0100 ffff  ..5.d...........
11 : 000000a0: fd97 3509 6400 0000 4c04 0000 0100 ffff  ..5.d...L.......
12 : 000000a0: 6c97 3509 6400 0000 b004 0000 0100 ffff  l.5.d...........
13 : 000000a0: 5feb 9513 6400 0000 1405 0000 0000 0100  _...d...........
16 : 000000a0: 5e7a 8313 6400 0000 4006 0000 0000 0100  ^z..d...@.......

Encore une fois je vous laisse regarder par vous même … Suite à de (très) longues recherches, plusieurs dizaines d'heures, j'ai fini par tout comprendre. Les 4 premiers octets (ex : 5e7a 8313) sont un indicateur de la date d'écriture, je n'ai pas réussi à convertir cette date en une donnée exploitable, et de toute façon ça n'aurait pour nos recherches actuelles pas vraiment d'intérêt. 6400 est une constante, elle est peut être utilisée lors d'un calcul mais je n'ai rien trouvé la concernant. Je ne m'y suis pas non plus vraiment attardé.

En observant les 4 derniers octets des fins de lignes, on peut observer une corrélation avec les dates (trié par valeur de date croissante) :

5feb 9513 : 0000 0100
5e7a 8313 : 0000 0100
...
4a11 1f17 : 0100 0100
...
fd96 3509 : 0100 ffff
6c97 3509 : 0100 ffff
bc97 3509 : 0100 ffff
fd97 3509 : 0100 ffff
9198 3509 : 0100 ffff
e298 3509 : 0100 ffff
3e98 3509 : 0100 ffff
4699 3509 : 0100 ffff
0c20 3909 : 0100 ffff
...
2734 3e26 : 0100 0100
c9c0 4126 : 0100 0100
ffbf 4126 : 0100 0100
3bbc 4126 : 0100 0100

Partie 4 : Stockage de la quantité d'argent

Most Significant Bits

Pour finir avec ce qui nous intéresse, la valeur 4006 représentait bien 0x16, mais comment ? J'ai essayé de modéliser plusieurs modèles, et j'ai finalement trouvé un modèle qui fonctionnait avec 3 opétations : multiplication, bit shift (exemple de l'opération bitshift pour un bitshift à gauche de 2: 0x10<<**2**=1010<<**2**=1010**00**=0x28), et un AND ( car la valeur maximale ne pouvait pas dépasser 16 bits.

Avec ces valeurs : Best fit found with factor=3940.00, shift=8, op=65535, j'obtenais les bonnes valeurs, mais sans les petits nombres à la fin (00, 01, 03, …). Voici une illustration du script python qui a calculé le modèle le plus proche :

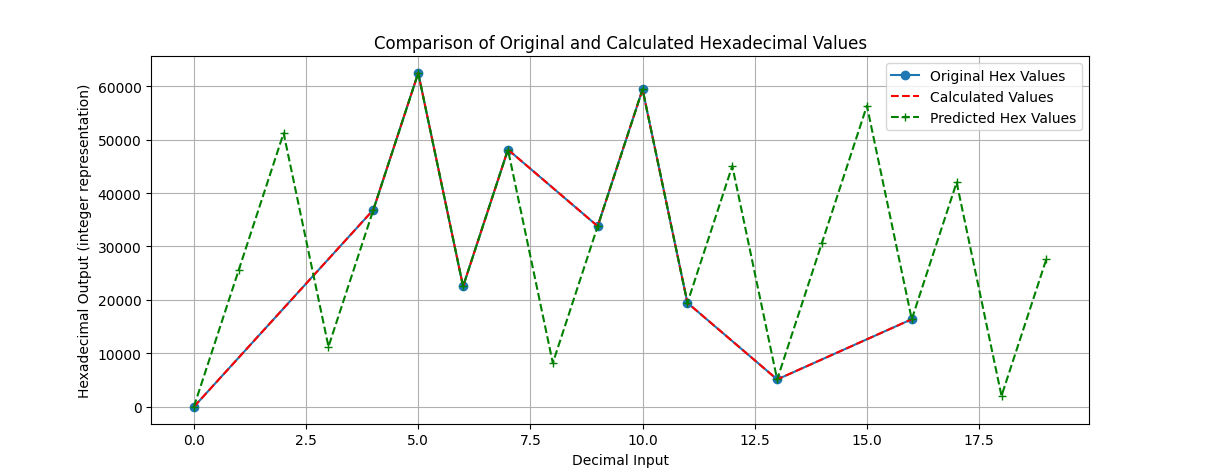
Least Significant Bits

J'ai ensuite regardé les bits de poids faible et je me suis rendu qu'ils semblaient être la partie entière, ou l'arrondi, d'une fonction affine, même peut être linéaire.

J'ai là aussi tenté plein de valeurs avant de trouver ce modèle :

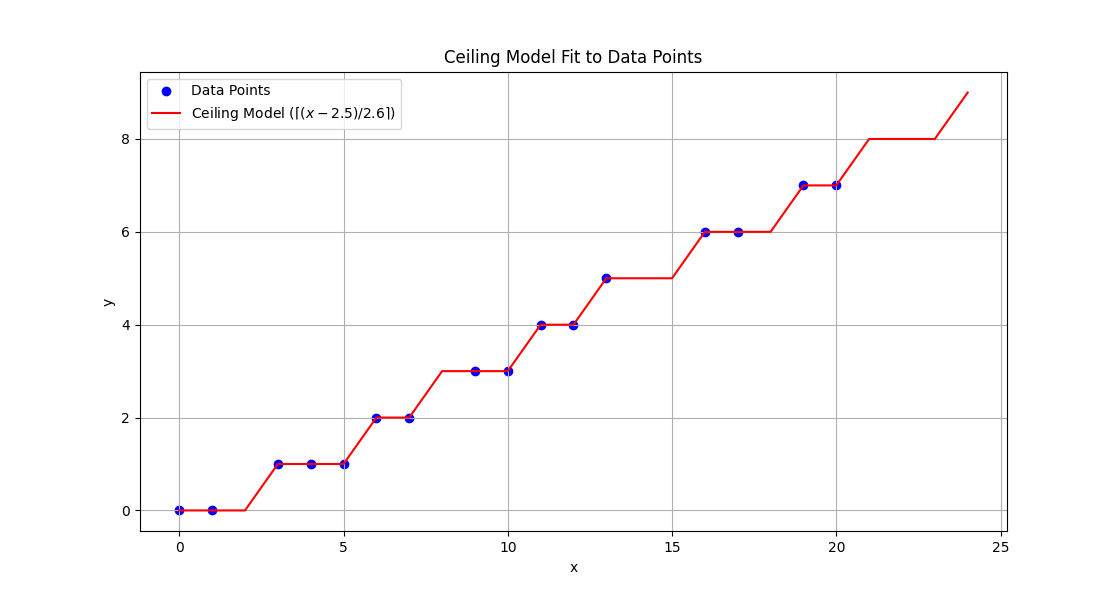
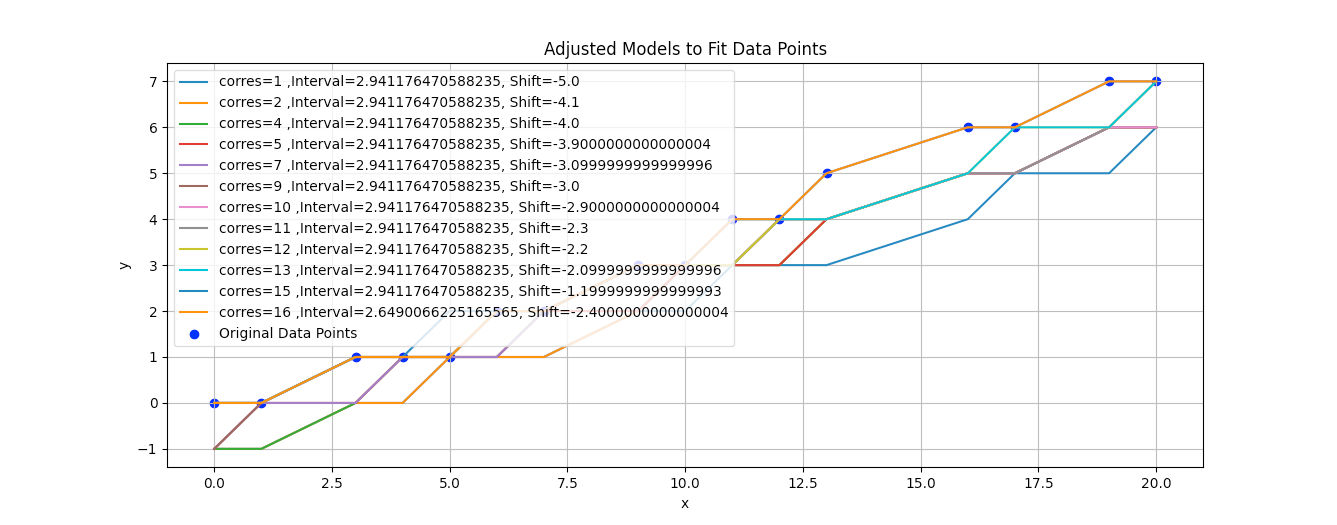
Cependant, tester toutes les possibilités est une méthode un peu brouillon… J'ai donc réalisé une deuxième version qui affichait les droites avec le plus petit et le plus grand coefficient directeur possible pour des fonctions linéaires :

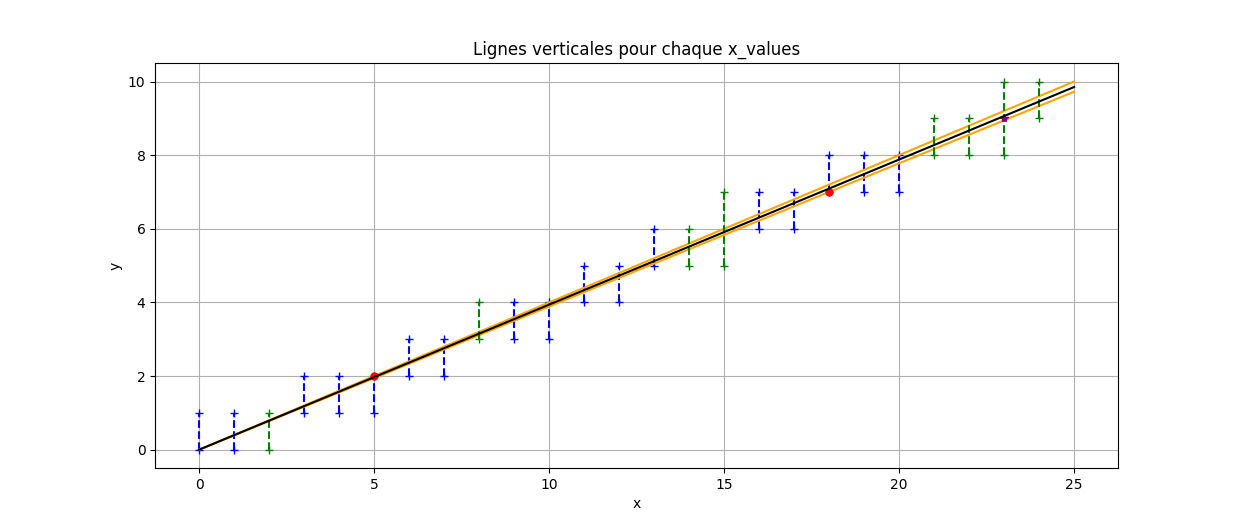
Légende de l'image : En rouge, on a les points qui définissent le min et le max. En bleu, ce sont nos données. En vert, nos prédictions. L'étoile violette signifie qu'il y a une incertitude sur la valeur.

Modèle final

Rendu ici, j'étais donc capable de mettre des valeurs comme 60€ alors que je n'avais jamais mis plus de 20€ sur ma carte ! Un peu après, j'ai remarqué que le coefficient directeur 1/0,3940 convenait tout à fait.

On peut donc approximer la valeur par y = ((x*3940)<<8)%65535 + (x/0,p3940)//1. On peut aussi simplifier (x*3940)<<8 par x*0x6400. % représente le reste de la division euclidienne, et // le quotient. En d'autres termes, on a y=(1008640*x)%65535 + (x/0,3940)//1.

Après ceci, j'ai essayé de mettre la valeur maximale possible sur la carte cashless. J'ai donc mis les least significant bits à 0xFF, et les most significant bits à la plus grande valeur possible (en restant dans la limite) : y = (x/0,3940)//1 = 0xFF=255<=> 256>(x/0,3940)≥255 <=> 649,7 > x ≥ 647,2.

J'ai donc choisi la valeur 649, soit 0x84ff. Après vérification du montant, il n'y avait en fait pas 649, mais 654.12€. Cela veut dire qu'il y a une imprécision dans un des calculs, elle pourrait venir du coefficient directeur que j'ai choisi.

Pour aller plus loin, voici un exemple de valeur assez particulière que j'ai essayé : 5d30 : 123€81.

Partie 5 : Conclusion et implications

Finalement, après avoir rendu mon rapport, l'entreprise m'a indiqué la raison pour laquelle mes calculs étaient incorrects. Pour stocker la valeur, celle-ci était multipliée par 100, puis les deux Bytes étaient échangés (ABCD → CDAB). Pour la valeur 5D30, on commence par inverser les deux bytes, ce qui donne 305D, puis on divise par 100, ce sui donne bien 123,81.

Après plusieurs tests et analyses, voici les principales vulnérabilités découvertes :

Clés de Chiffrement Non-Sécurisées : Les cartes utilisées (MIFARE Classic 1k) sont vulnérables, les clés de chiffrement peuvent être trouvées. Le principe même d'une clé est d'être secrète, la ce n'est pas le cas du tout... Cela permet à un attaquant de lire et modifier les données stockées sur la carte.

Manipulation des Données de la Carte : Les valeurs de solde sur la carte peuvent être modifiées à l'aide d'outils de hacking NFC comme le Proxmark3, mais un téléphone sous Android suffit tout à fait.. Cela signifie qu'un attaquant peut créditer des montants fictifs sur la carte, compromettant ainsi l'intégrité des transactions.

Vulnérabilités dans l'Écriture et la Lecture : Les informations telles que les dates d'écriture et d'autres métadonnées peuvent être manipulées, ce qui pourrait éventuellement compromettre la fiabilité des transactions.